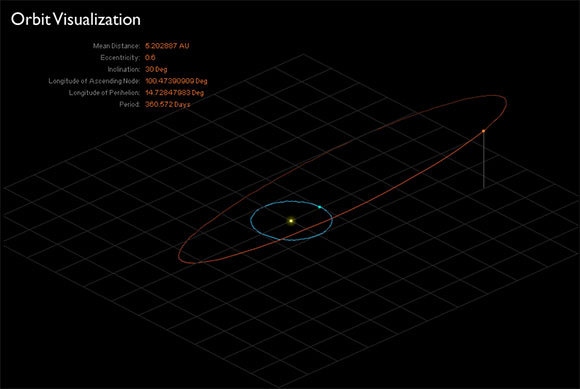
I finished a first experiment. I think I have the code for the orbits almost done. It’s still very slow and user-unfriendly. But you can change the orbit of the orange planet already.
If you are interested, the function I was looking for goes almost something like this (AS3 code):
public const TORADIANS:Number = (Math.PI / 180);
public function stateVector(t:Number, o:orbit):point3D {
// Calculates the State Vector (xyz coordinates)
// of an object in an orbit at a given Time
// The coordinate system is Heliocentric
// and aligned to the eclyptc
// t - current time (in days)
//o.e - Eccentricity (degrees)
//o.a - Mean Distance (Astronomical Units)
//o.i - Inclination (degrees)
//o.O - longitude of ascending node (degrees)
//o.w - longitude of perihelion (degrees)
//o.P - Period (days)
// Define some Variables to work with
var myX:Number;
var myY:Number;
var myZ:Number;
var M:Number;
var V:Number;
var r:Number;
// Choose a Mean Anomaly
// This is due to change
// Right now, all Planets start at 0° at t=0
M = ((t / o.P) - int(t / o.P));
M = M * 360;
// Calculate True Anomally
V = getTrueAnomaly(M, o.e);
// Calculate Radial Distance
r = (o.a * (1-o.e*o.e)) / (1 + o.e * Math.cos(V * TORADIANS));
// Transform Orbital Coordinates into
// Heliocentric Ecliptic coordinates
// Sin / Cos values are pre-calucated to save redundancy
var sinWV:Number = Math.sin((o.w+V)*TORADIANS);
var cosWV:Number = Math.cos((o.w+V)*TORADIANS);
var sinI:Number = Math.sin(o.i*TORADIANS);
var cosI:Number = Math.cos(o.i*TORADIANS);
var sinO:Number = Math.sin(o.O*TORADIANS);
var cosO:Number = Math.cos(o.O*TORADIANS);
// Calulacte Carthesian Coordinates
myX = r * (cosO*cosWV - sinO*sinWV*cosI);
myY = r * (sinO*cosWV + cosO*sinWV*cosI);
myZ = r * sinWV * sinI;
// And that's where the Planet is
return new point3D(myX,myY,myZ);
}
public function getTrueAnomaly(M:Number, e:Number):Number {
// Approximates the True Anomaly (V) from the Mean Anomaly (M)
// Set constants for precision approximation
const TOLERANCE:Number = 1.0e-12;
const MAXAPPROX:int = 80;
// Some Variables
var E1:Number;
var E2:Number;
var V:Number;
// Convert from Degrees to Radians
M = M * TORADIANS;
// First calculate the Eccentric Anomaly
// Get a first approximation for the Eccentric Anomaly
E1 = M;
// Start iterating to calculate a closer value
var loopCount:int = MAXAPPROX;
do {
E2 = E1;
E1 = M + e * Math.sin(E2);
// Quit loop if close enough or running too long already
} while (Math.abs(E1 - E2) > TOLERANCE && --loopCount > 0);
// Now convert Eccentric Anomaly to True Anomaly
V = 2 * Math.atan(Math.sqrt((1+e)/(1-e)) * Math.tan(E1 / 2));
// Convert back to degrees
V = V / TORADIANS;
// And that's the True Anomaly
return V;
}
I still need to tie the place in orbit to a REAL time and date. That problem is related the the last post. But now that I got a prototype, I should be able to experiment to figure it out. I will also improve the performance and interface so people can use this app for their own experiments.






because i just used the java code and did not even try to understand the math behind it, there is not much i can add to this
besides that either the data is flawed, the math inside my aplett is buggy or the whole thing is like it is – after a couple of thousands of years (backward or forward) the trojans and greeks just ungroup and float arround the sun (at their initial distance) in a rather random order (and not sticking to the initial groups as i expected)
lets wait until you have your toy filled with them and are running a timewarp … probably its a precision problem? i’m pretty sure the java aplett code was running with double floating point precision … and i thought that must be sufficient
I don’t think your applet is simulating stuff like Orbital Precession or gravitational influences from other bodies. Actually, it is the influence of Jupiter that keeps the Trojans together. The only solution to that problem is to make a proper gravity simulation like this http://www.orbitsimulator.com/gravity/articles/what.html
But even software like this isn’t perfect and every orbit simulation will get imprecise in the long-term.
But for Sci-Fi purposes, 1000 years should be more than enough.
ah, okay … makes sense
i somewhat stupidly assumed all those mathematical details from nasa include all thats necessary for a huge amount of years (until galacitcal proportions come into play)
i checked it again, actually it looks like it doesn’t even hold 100 years :-/
nevertheless, i believe creating a game from this will be difficult, because of the totaly unclear motions of objects, you will not be able to do most basic 4X or settlement game features, but instead hard-scifi-like the player needs to cope a lot with movement basics (i.e. which astroid will be in range, when)
for my personal style of game, this seems to become very complex quickly …